カメラの撮影範囲を計算して可視化する

山本紘暉

2023.07.03

この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。

はじめに

新規事業統括部 Passregiチームの山本です。

PassregiのCVチームでは、カメラを使った人物追跡システムを作成しています。今までは様々な改良をしてきたのですが、詳しい内容については、以下のページをご覧ください。

https://dev.classmethod.jp/articles/developers-io-day-one-passregi-cv-improvements/

こうしたカメラを使ったシステムでは、カメラの位置や向きを計測するキャリブレーションという作業が必要です。

このページでは、キャリブレーション後に、以下のような項目を確認する方法として、カメラのカバー範囲を計算（可視化）する方法について記載します。

カバーできているか、弱そうな箇所がないか
カメラの台数を増やした方が良い箇所はどこか

最初に考え方や計算方法の式について記載し、最後にサンプルコードと実際の値を使って計算した結果を記載します。

お詫び

DevelopersIOでは数式が表示できないという問題があります。数式もご覧になりたい方は、zennの記事をご覧ください。

https://zenn.dev/cm_yamahiro/articles/calc_and_visualize_camera_capture_area

考え方

計算方法の前に考え方について説明します。

前提の説明

以下のようなシステムを想定しています。下2つに関してはPassregiCV特有の内容です。

カメラを天井に設置してあり、床を見下ろす向きになっている
カメラで撮影した映像（画像）を、骨格検出モデルに入力し、写っている人の骨格を得ている
- 人物ごとに、頭・首・両肩・両肘・両手首がどこにあるかがわかる
現状では頭や肩を使って追跡している
- 肩は頭より低い位置にあるので、撮影できる範囲はより広くなる。なので、頭が映る範囲がカバーできていれば、肩もカバーできていることになる（頭の映る範囲を考えればよい）。

今回のゴール

上記の前提から、システム全体での撮影範囲を可視化するには、それぞれのカメラでどの範囲まで頭が撮影できるかを計算し、それらを重ね合わせれば良さそうです。

よって、以降はそれぞれのカメラである高さ（頭の高さ）が一定である平面（z=z0）が写っている範囲（座標）を考えます。

計算方法

まずは、定義に基づいて、どのようにすれば目的の座標が得られるかの計算方法について説明します。

（カメラの内部パラメータ・外部パラメータは既知（キャリブレーション済み）であるとします。それぞれのキャリブレーション方法については、OpenCVのページや以前の記事をご覧ください。）

https://dev.classmethod.jp/articles/estimate-camera-external-parameter-matrix-2d-camera/

歪みがない場合

範囲

歪みがない場合、（各計算は線形であるため）カメラの四隅がz=z0の平面上に対応する座標を計算し、それらを繋げた四角形が撮影範囲です。

計算方法

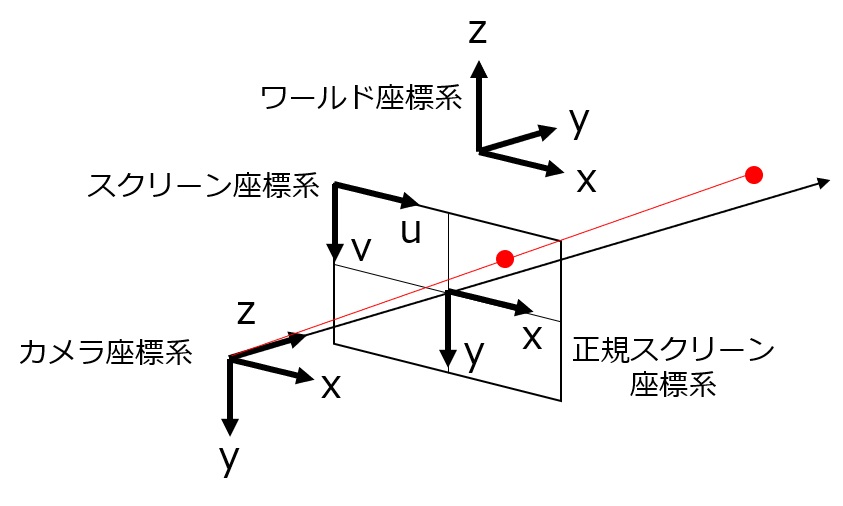
定義

K：カメラの内部パラメータ
R：カメラの外部パラメータ（回転行列）
t：カメラi外部パラメータ（並進ベクトル）
※ R・tは一般の定義と異なります
c_w：ある点pのワールド座標
c_c：カメラからみた、pのカメラ座標
c_s：カメラからみた、pのスクリーン座標
λ：定数

$$ \begin{aligned}

K &= \mathbb{R}^{3 \times 3}\ R &= \mathbb{R}^{3 \times 3} \ t &= \mathbb{R}^{3} = \begin{pmatrix} t_x \ t_y \ t_z \end{pmatrix} \ c_w &= \begin{pmatrix} x \ y \ z \end{pmatrix} \ c_{c} &= \begin{pmatrix} x_{c} \y_{c} \ z_{c} \end{pmatrix} \ c_{s} &= \begin{pmatrix} u \v \ 1 \end{pmatrix} \ c_w &= R c_c + t \ \lambda c_s &= K c_c \end{aligned}

これを式変形すると

$$ \begin{aligned} c_w &= Rc_c + t \ &= R(\lambda K^{-1}c_s) + t \ &= \lambda RK^{-1}c_s + t \end{aligned} $$

ここでM（3x3行列）と、m_0・m_1・m_2（1x3行列）を以下のように定義します

$$ \begin{aligned} M &= \begin{pmatrix} -m_0- \ -m_1- \ -m_2- \end{pmatrix} \ &= RK^{-1} \ \end{aligned} $$

これで上の式を置き換えると以下のようになり、画像上のある点の座標c_sとそれに対応する空間上の座標c_w=(x,y,z)の関係が得られます。（m_nは1行3列、c_sは3行1列であるため、m_n c_s はスカラー値です）

$$ \begin{aligned} c_w &= \lambda Mc_s + t \ \begin{pmatrix} x \ y \ z \end{pmatrix} &= \lambda \begin{pmatrix} -m_0- \ -m_1- \ -m_2- \end{pmatrix} c_s + t \ \begin{pmatrix} x \ y \ z \end{pmatrix} &= \lambda \begin{pmatrix} m_0 c_s + t_x \ m_1 c_s + t_y \ m_2 c_s +t_z \end{pmatrix} \end{aligned} $$

よって、ある高さの平面z=z0に作る平面上の点（x,y）と、c_sとの関係は以下のとおりです。

$$ \begin{aligned}

\begin{pmatrix} x \ y \ z_0 \end{pmatrix} &= \lambda \begin{pmatrix} m_0 c_s + t_x \ m_1 c_s + t_y \ m_2 c_s +t_z \end{pmatrix} \ \lambda &= \frac{z_0-t_z}{m_2c_s} \ \begin{pmatrix} x \ y \end{pmatrix} &= \frac{z_0-t_z}{m_2c_s} \begin{pmatrix} m_0 c_s + t_x \ m_1 c_s + t_y \end{pmatrix}

\end{aligned} $$

画像上の点を(u_0, v_0)としたとき、対応する点(x_0, y_0)は以下のように計算できます。

$$ \begin{aligned}

\begin{pmatrix} x_0 \ y_0 \end{pmatrix} &= \frac{z_0-t_z}{m_2 \begin{pmatrix} u_0 \ v_0 \ 1 \end{pmatrix}} \begin{pmatrix} m_0 \begin{pmatrix} u_0 \ v_0 \ 1 \end{pmatrix} + t_x \ m_1 \begin{pmatrix} u_0 \ v_0 \ 1 \end{pmatrix} + t_y \end{pmatrix}

\end{aligned} $$

歪みがある場合

範囲

線形ではないので、四隅の計算だけでは範囲が本来の範囲とずれてしまいます。厳密にやるなら、撮影範囲の四辺をできる限り細かく分割し、それぞれの点がz=z0の平面上に対応する点を繋ぐことで撮影範囲を得られます。

図を追加する

計算方法

歪みがある画像での座標を(u_0’, v_0’)とした時、歪みを補正した後の座標(u_0, v_0)を上の式に代入すれば計算できます。

$$ \begin{aligned}

\begin{pmatrix} u_0 \ v_0 \end{pmatrix} &= \text{undistort}( \begin{pmatrix} u_0' \ v_0' \end{pmatrix} ) \ \begin{pmatrix} x_0 \ y_0 \end{pmatrix} &= (上記の式)

\end{aligned} $$

歪みの補正は歪みモデルによって変わるので、ここでは一つの関数として表しました。実際の処理方法などは次節の計算コードをご覧ください。

サンプルの計算と工夫点

使用したコード

必要なライブラリは以下のとおりです。

pip install opencv-python
pip install numpy

使用したコードは以下のとおりです。

import enum
from typing import List, Optional, Tuple

import cv2
import numpy as np

class CalcAreaType(enum.Enum):
    """CalcAreaType is enum class of calc_area function"""

    RECTANGLE_SIMPLE = enum.auto()  # calc four corners of image (for not distorted image)
    RECTANGLE_STRICT = enum.auto()  # calc divided points on four edges of image (for distorted image)
    OCTAGON = (
        enum.auto()
    )  # calc four corners narrowed to center and middle points of four edges to avoid strong distortion (for distorted image)

COLORS = [
    (0, 0, 0),  # black
    (0, 0, 200),  # red
    (0, 200, 200),  # yellow
    (0, 255, 00),  # green
    (200, 200, 0),  # cyan
]

def project_to_plane(
    point: np.ndarray,
    K: np.ndarray,
    R: np.ndarray,
    t: np.ndarray,
    z0: float,
):
    point_vec = np.array([point[0], point[1], 1]).reshape((3,))

    K_inv = np.linalg.inv(K)
    M = R @ K_inv
    m0 = M[0, :]
    m1 = M[1, :]
    m2 = M[2, :]

    llambda = (z0 - t[2]) / np.dot(m2, point_vec)
    x = (t[0] + np.dot(m0, point_vec) * llambda)[0]
    y = (t[1] + np.dot(m1, point_vec) * llambda)[0]

    return np.array([x, y, z0]).reshape((3, 1))

def calc_correspoinding_point(
    u: float,
    v: float,
    K: np.ndarray,
    distortion_coeffs: Optional[np.ndarray],
    R: np.ndarray,
    t: np.ndarray,
    z0: float,
):
    # undistort point if distortion coefficients is given
    if distortion_coeffs is None:
        point = [u, v]
    else:
        point_: np.ndarray = cv2.undistortPoints(
            np.array([u, v], dtype=np.float32).reshape((2,)),  # input as (2 x n) matrix
            cameraMatrix=np.array(K),
            distCoeffs=np.array(distortion_coeffs).reshape((1, 5)),
            # P=newcameramtx,
            P=np.array(K),
            # R=np.array(self.K),
        )
        point = point_[0][0]

    # calc corresponding point on plane
    point_on_plane = project_to_plane(
        point=np.array(point),
        K=K,
        R=R,
        t=t,
        z0=z0,
    )
    return point_on_plane

def estimate_camera_area(
    image_size: Tuple[float, float],  # (width, height)
    K: np.ndarray,  # intrinsic matrix (3 x 3)
    distortion_coeffs: Optional[np.ndarray],  # distortion coefficients (4~8)
    R: np.ndarray,  # rotation matrix (3 x 3)
    t: np.ndarray,  # translation vector (3 x 1)
    z0: float,  # height of plane to calc area
    calc_area_type: CalcAreaType,
    n_devide_edge: int = 10,
):
    w, h = image_size

    # decide point to calc according to calc_area_type
    if calc_area_type == CalcAreaType.RECTANGLE_SIMPLE:
        image_coords = [
            [0, 0],  # left top
            [w, 0],  # right top
            [w, h],  # right bottom
            [0, h],  # left bottom
        ]
        # calc four corners of image (for not distorted image)
    elif calc_area_type == CalcAreaType.RECTANGLE_STRICT:
        # devide edge
        image_coords = sum(
            [
                [(i * w / n_devide_edge, 0) for i in range(n_devide_edge)],  # top edge
                [(w, i * h / n_devide_edge) for i in range(n_devide_edge)],  # right edge
                [(w - i * w / n_devide_edge, h) for i in range(n_devide_edge)],  # bottom edge
                [(0, h - i * h / n_devide_edge) for i in range(n_devide_edge)],  # left edge
            ],
            [],
        )
    elif calc_area_type == CalcAreaType.OCTAGON:
        image_coords = [
            [w * 1 / 8, h * 1 / 8],  # left top
            [w / 2, 0],  # top
            [w * 7 / 8, h * 1 / 8],  # right top
            [w, h / 2],  # right
            [w * 7 / 8, h * 7 / 8],  # right bottom
            [w / 2, h],  # bottom
            [w * 1 / 8, h * 7 / 8],  # left bottom
            [0, h / 2],  # left
        ]
    else:
        raise ValueError(f"calc_area_type {calc_area_type} is not supported")

    # calc coordinate on z=z0 plane
    area_points = [
        calc_correspoinding_point(
            image_coord[0],
            image_coord[1],
            K,
            distortion_coeffs,
            R,
            t,
            z0,
        )
        for image_coord in image_coords
    ]
    return area_points

def draw_camera_area(
    image_coverage: np.ndarray,  # (h,w) uint8
    area_points: List[np.ndarray],
    display_scale: float,
):
    area_points_scaled = [(point[:2].reshape((2,)) / display_scale).astype(np.int32) for point in area_points]
    # draw area
    cv2.fillPoly(
        image_coverage,
        np.array([area_points_scaled]),
        color=1,
    )

def display(
    display_img_size: Tuple[int, int],
    display_scale: float,
    area_points_list: List[List[np.ndarray]],
):
    image_coverage = np.zeros((display_img_size[1], display_img_size[0]), np.uint8)
    for area_points in area_points_list:
        draw_camera_area(image_coverage, area_points, display_scale)

    img_coverage_color = np.zeros(
        (
            int(display_img_size[1]),
            int(display_img_size[0]),
            3,
        ),
        dtype=np.uint8,
    )

    for i, color in enumerate(COLORS):
        if i == 0:
            continue

        if i = i
        img_coverage_color += np.dstack([image_display_i, image_display_i, image_display_i]) * np.array(color).astype(
            np.uint8
        )

    cv2.imshow("image", img_coverage_color)
    cv2.waitKey(0)

def main(
    image_size: Tuple[float, float],  # (width, height)
    K: np.ndarray,  # intrinsic matrix (3 x 3)
    distortion_coeffs: Optional[np.ndarray],  # distortion coefficients (4~8)
    R: np.ndarray,  # rotation matrix (3 x 3)
    t: np.ndarray,  # translation vector (3 x 1)
    z0: float,  # height of plane to calc area
    calc_area_type: CalcAreaType,
    display_img_size: Tuple[int, int],
    display_scale: float,
):
    area_points = estimate_camera_area(
        image_size=image_size,
        K=K,
        distortion_coeffs=distortion_coeffs,
        R=R,
        t=t,
        z0=z0,
        calc_area_type=calc_area_type,
    )

    display(
        display_img_size=display_img_size,
        display_scale=display_scale,
        area_points_list=[area_points],
    )

if __name__ == "__main__":
    # target plane hight [mm]
    z0 = 1800.0

    # camera parameters
    image_size = (480, 270)
    K = np.array(
        [
            [271.7, 0.0, 240.0],
            [0.0, 271.7, 135.0],
            [0.0, 0.0, 1.0],
        ]
    )
    distortion_coeffs = np.array([-0.32, 0.127, 0.002, 0.0, -0.027])
    R = np.array(
        [
            [-0.991371159836129, 0.1195736688408402, -0.0537155579428299],
            [-0.1310310030769523, -0.9156816133144915, 0.3799448108218059],
            [0.0037549537701762, -0.3837047312162194, -0.9234482008020115],
        ]
    )
    t = np.array(
        [
            8352.517961479696,
            955.2394122989581,
            2942.0001773865256,
        ]
    ).reshape((3, 1))

    # calc_area_type = CalcAreaType.RECTANGLE_SIMPLE
    # calc_area_type = CalcAreaType.RECTANGLE_STRICT
    calc_area_type = CalcAreaType.OCTAGON

    # display
    display_img_size = (1000, 800)  # image_size of display (width, height(
    display_scale = 10.0  # scale to display (divide coord by this value)

    # execute
    main(
        image_size=image_size,
        K=K,
        distortion_coeffs=distortion_coeffs,
        R=R,
        t=t,
        z0=z0,
        calc_area_type=calc_area_type,
        display_img_size=display_img_size,
        display_scale=display_scale,
    )

このコードでは、カメラのパラメータをもとに、撮影範囲を上からみた画像（XY平面）に描画して表示します。Kが内部パラメータ、distortion_coeffsが歪みパラメータの係数、Rが外部パラメータの回転行列、tが外部パラメータの並進ベクトルです。

（OpenCVの定義（cv2.solvePnPで出力されるrvec、tvec）と合わせる場合は、以下のようにしてください）

https://dev.classmethod.jp/articles/estimate-camera-external-parameter-matrix-2d-camera/#toc-6

R_mat, _ = cv2.Rodrigues(rvec)
R = R_mat.T
t = -R_mat.T @ tvec

project_to_plane関数・calc_correspoinding_point関数が前節で説明した計算です。estimate_camera_area関数では指定された計算方法によって、計算するべき点を決めています（詳細は次項で説明）。

display関数では、計算した撮影範囲を画像に表示し、その撮影範囲のカバー数をもとに色分けして表示してます（次節で使用）。

今回指定したカメラのパラメータは、天井に下向き（鉛直線から約20度前向き）に取り付けたカメラです。

結果と改善点

上記のコードの250～252行目について説明します。計算に使用する点をパラメータとして設定しています。

RECTANGLE_SIMPLE
画像の四隅の点のみを計算して、つなぎ合わせた方法です。ただし、「計算方法」の節で説明したとおり、歪みがあるカメラの場合、実際の範囲と大きく異なってしまいます。

RECTANGLE_SIMPLEの場合

RECTANGLE_STRICT
画像の四辺を分割して、それぞれが対応する点を計算して、つなぎ合わせた方法です。カメラのパラメータ（特に歪みのパラメータ）が正確であれば、この範囲が正しい撮影範囲になります。ただし、キャリブレーションの精度が低い場合、特に四隅近くの点に大きなズレが生じやすくなります。実際に、下の図のようには撮影はできていません。

RECTANGLE_STRICTの場合

OCTAGON
上記のようにキャリブレーションの精度に依存すること加え、骨格検出も画面の四隅だと歪みの影響で精度が下がるという問題があるため、四隅を少し削った八角形で撮影範囲を計算するようにしました（四隅から画像のサイズの1/8ずつ中心に移動しました）。すると以下の図のようになり、妥当な範囲になりました。（なので、歪みが強いカメラやキャリブレーションの精度が高くない状況では、この方法がオススメです）

八角形を図示すると、2つ目の図の範囲です。

OCTAGONの場合

自社の模擬店舗で図示した結果

クラスメソッドでは自社内に模擬店舗のスペースを用意し実験を行っています（現在はオフィス移転にともない準備中、7月再開予定）。複数のカメラを設置してキャリブレーションを行ったため、その範囲を可視化してみました（複数カメラの範囲を表示するように、上記のコードを少し改良しました）。

結果は下図のとおりです。店内の画像と全部のカメラ（55台）のカバー範囲の図を重ね合わせたものです。店内の画像はiPad（LiDAR）を使ってスキャンし、3DモデルをUnreal Engineに取り込んで上からのカメラ（Top View）でレンダリングした画像です。

それぞれの色は以下を表しています。カッコ内は追跡に必要なカメラの数から見た過不足です。

赤色：1つのカメラでカバーしている（足りない）
黄色：2つのカメラでカバーしている（ギリギリ足りている、精度が落ちる可能性がある）
緑色：3つのカメラでカバーしている（足りている）
水色：4つ以上のカメラでカバーしている（十分）

図から以下のことが分析できました。

全体的には4つ以上のカメラでカバーできていて十分そう
一部（右下の黄色になっている箇所）は精度が落ちる要因になっている可能性がある

まとめ

カメラのキャリブレーション結果やカバー範囲を確認するために、カメラの撮影範囲を計算し可視化する方法を説明し、コードで実装しました。キャリブレーションの精度や検出の精度に対応した計算方法を考えました。実際の模擬店舗のデータで撮影範囲を可視化し、分析に使用できることを確認しました。

調べていると、意外とまとまった説明がなかったので、記事にしてみました。

付録

キャリブレーション結果の歪みパラメータで、撮影画像をシミュレートした結果
こちらのリポジトリで公開されているコードを、一部変更して利用させていただきました

https://github.com/kamino410/cv-snippets/

実際にカメラで撮影した画像

シミュレート上では（今回使用したパラメータでは）カメラの端っこが強く歪んでいますが、実際の画像ではそこまで歪んでいません。そのため、RECTANGLE_STRICTのようにおかしな結果になってしまいました。

カメラの端の部分まで正確になるように（内部パラメータを）キャリブレーションできれば、RECTANGLE_STRICTでも良いかと思いますが、実際のカメラでやってみると正確なキャリブレーションは結構難しかったので、今回の工夫のように端っこは使用しない方法（OCTAGON）のように計算するのが良さそうです。